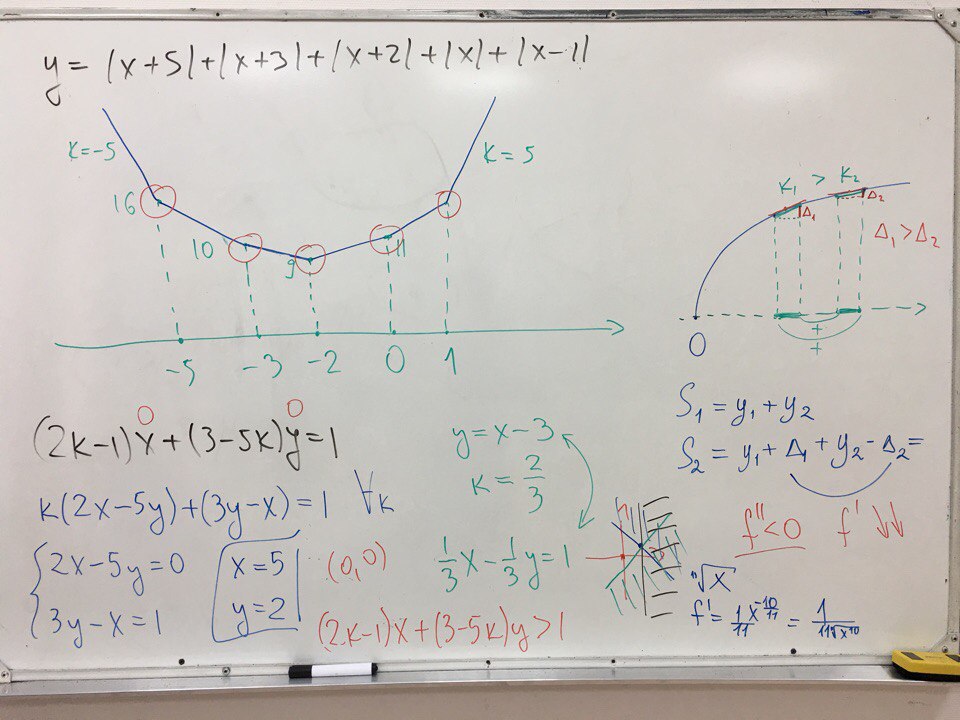
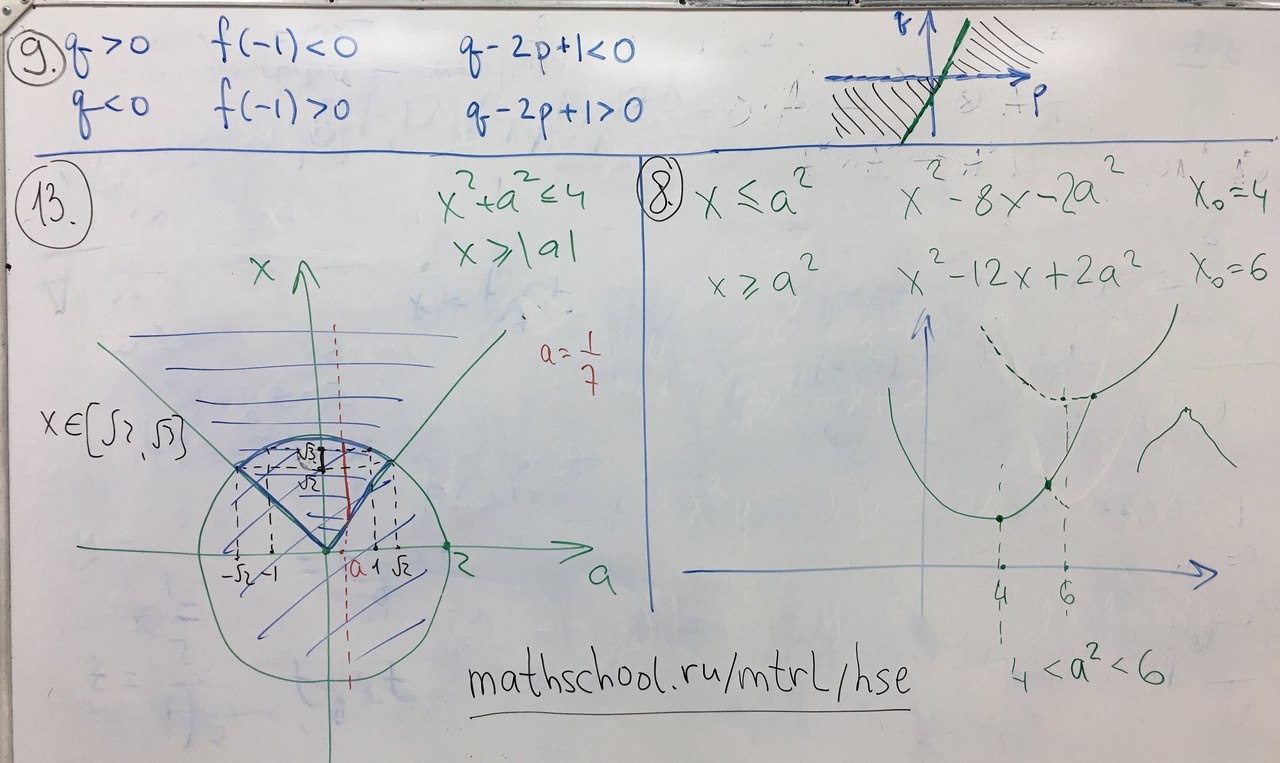
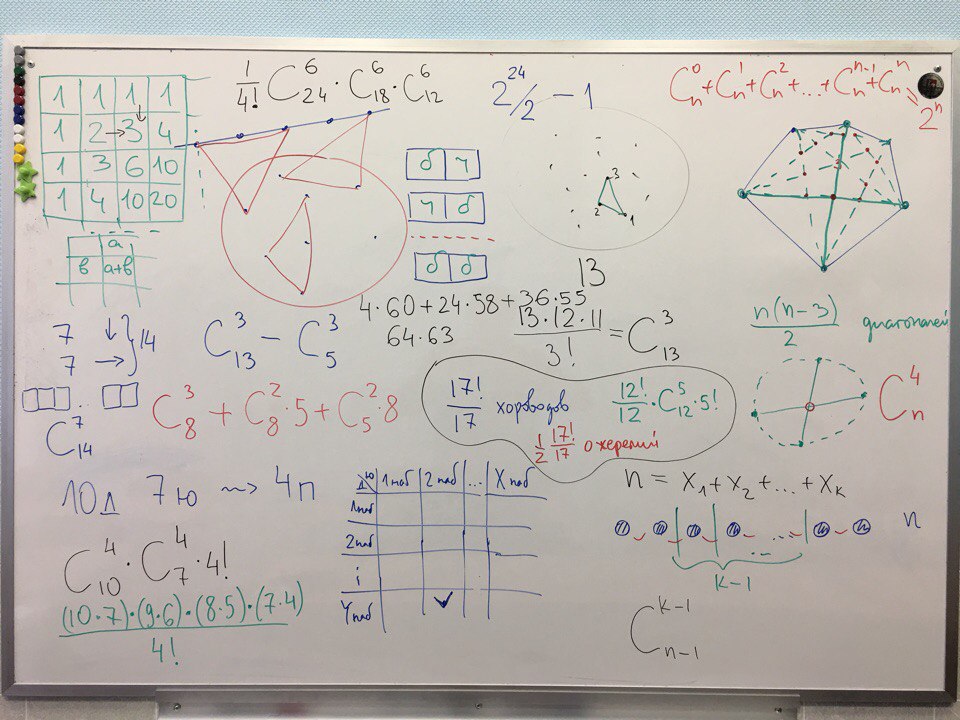
Творчество лицеистов

"Комплексные числа в задачах планиметрии" (Мария Петрова, выпуск 2019)

В средней школе вы узнали о новом виде уравнений – квадратные уравнения. Для их решения вы использовали всем известную формулу дискриминанта. Однако когда дискриминат был меньше нуля, вам говорили, что уравнение не имеет корней. Но это не так! Внесём маленькую поправку: уравнение в данном случе не имеет действительных корней. Как же тогда решать такие уравнеия? Ответ прост: с помощью комплексных чисел. Комплексные числа – это новое множество чисел, которое содержит в себе множество вещественных чисел. Особенно часто применяются формулы комплексного переменного, в частности, аналитические функции: они используются в механике, аэро- и гидродинамике, в алгебраической и неевклидовой геометрии, теории чисел. Вместе с тем алгебру комплексных чисел можно успешно использовать и в более простых разделах математики: элементарной геометрии, тригонометрии, теории движений и подобий, аффинных и круговых преобразований, а также в различных механических и физических задачах. Данное пособие поможет читателю разобраться с основными свойствами комплексных чисел и их применением на практике. В данной книге содержатся два раздела, один из которых расскажет об арифметических действиях над комплексными числами, а второй – о применении комплексных чисел в планиметрии.

Скачать текст