О проблеме Варинга (элементарные методы)

В 1770 г. Ж. Л. Лагранж доказал, что каждое натуральное число есть сумма не более четырех квадратов натуральных чисел. В том же году Е. Варинг высказал предположение, что каждое натуральное число есть сумма не более 9 кубов натуральных чисел, не более 19 биквадратов и т. д. Первый шаг в решении этой проблемы сделал в 1859 г. Ж. Лиувилль, доказавший, что каждое натуральное число есть сумма не более 53 биквадратов. Доказательство опирается на теорему Лагранжа и тождество

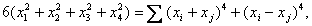
в котором суммирование ведется по всем парам целых чисел i, j 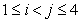. Впоследствии усилиями многих математиков предположение Варинга было доказано для 3, 5, 6, 7, 8, 10 степеней. При этом использовались все более сложные тождества, подобные приведенному. В 1909 г. Д. Гильберт доказал, что

при любом целом 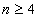каждое натуральное число допускает представление в виде суммы n -x степеней натуральных чисел, количество которых не превосходит некоторой границы, определяемой только показателем n, и не зависит от представляемого числа.

В настоящее время известны несколько различных элементарных доказательств этого утверждения.

В связи с проблемой Варинга возникло множество различных вопросов, часть из них, несмотря на усилия выдающихся математиков, не имеет решения и до сих пор. Проблема Варинга породила множество интересных работ и способствовала развитию как теории чисел, так и теории функций.

В докладе будет рассказано о некоторых идеях, возникших в связи с исследованиями проблемы Варинга, о результатах, доказываемых в этом направлении вплоть до последнего времени. Мы сосредоточимся в основном на элементарных методах. Никаких специальных знаний от слушателей не предполагается.