Открытый московский турнир математических боев

С подробной информацией можно ознакомиться на официальном сайте турнира: http://olympiads.mccme.ru/matboi/.

Регламент турнира

Математические бои – устное командное соревнование по математике для школьников старших классов. Московский открытый турнир математических боёв проводится по инициативе Московского центра непрерывного математического образования совместно с учителями математики Москвы при поддержке МИОО.

Решение задач, предлагаемых на турнире, не требует знаний сверх школьной программы, но требует нестандартного мышления, умения работать коллективно и, как всякое соревнование, – выдержки и воли к победе.

Турнир проводится для 8–11 классов, в каждой параллели - две лиги, отличающиеся по сложности задач. Задачи лиги А – существенно более сложные и предназначены для команд, имеющих успешный опыт участия в официальных турнирах математических боев.

Участие в турнире бесплатное.

В турнире могут участвовать как московские команды, так и команды из Подмосковья и других регионов.

Турнир включает в себя три этапа:

1) Устная командная олимпиада.

По итогам командной олимпиады в каждой лиге каждого класса выделяются по 4 команды, показавшие наилучшие результаты. Эти команды в последующих двух этапах разыгрывают Кубок Лиги, для остальных команд следующие этапы являются тренировочными.

2) В рамках каждой лиги проходит первый тур математических боев (см. правила): для 4 команд – полуфинальные бои, для остальных команд – тренировочные.

Состав полуфинальных пар определяет оргкомитет. Места проведения полуфиналов объявляются отдельно.

Команды, пожелавшие участвовать в тренировочных боях (по тем же вариантам!), договариваются между собой (электронная база по каждой лиге доступна всем заявившимся командам) и проводят эти бои на своих территориях. Эти бои обеспечиваются судьями, если они проходят в черте г. Москвы и если заявка на судей подана заблаговременно.

3) В рамках каждой лиги проходит второй, заключительный тур математических боев: для победителей полуфиналов – финальные бои, для проигравших полуфиналы – бой за III место; для остальных команд – тренировочные. Места проведения финальных боев и состав жюри определяет оргкомитет.

Команды, пожелавшие участвовать в тренировочных боях (по тем же вариантам!), договариваются между собой (электронная база по каждой лиге будет доступна всем заявившимся командам) и проводят эти бои на своих территориях. Эти бои обеспечиваются судьями, если эти они проходят в черте г. Москвы и если заявка на судей подана заблаговременно.

Победители финальных боев награждаются дипломами и призами.

В Турнире может принять участие любая команда школьников 8–11 классов в составе от 6 до 12 человек. При этом, в каждом из этапов могут участвовать не более 8 школьников и только из числа внесенных в заявку. Со всеми вопросами, возникшими у вас по поводу турнира, Вы можете обратиться в оргкомитет по электронной почте по адресу matboi@mccme.ru, по телефону 241-1237, или к координатору Турнира Блинкову Александру Давидовичу: blinkov@mccme.ru, 976-1985 (понедельник, вторник, пятница с 16.00 до 18.00).

СУНЦ МГУ заявил команды СУНЦ-11 (11 класс) и СУНЦ-10 (10 класс) в лигу А турнира

Приведем составы команд:

Командная олимпиада

По итогам командной олимпиады команда СУНЦ-11 заняла 4 место и продолжила борьбу в лиге А 11 класса!

Общие результаты в лиге А 11 класса:

В полуфинальном бою 19 ноября команде СУНЦ-11 предстояло встретится с командой "57-11D" (капитан: Аня Боярченкова).

Команда же СУНЦ-10, заняв 5 место в лиге, к сожалению, выбыла из турнира.

Общие результаты в лиге А 10 класса:

Заметим, что обе команды СУНЦ не смогли выставить оптимальные составы на командную олимпиаду, так как сильнейшие 10- и 11-классники в это же время представляли СУНЦ на XVII Российском Фестивале юных математиков, проходившем в г. Адлере.

Приведем условия задач:

Лига 10А

1. Верно ли, что для любого x>= 1 ?

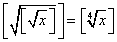2. Дан треугольник ABC. Две прямые, симметричные прямой АС относительно прямых АВ и ВС соответственно, пересекаются в точке К. Докажите, что прямая ВК проходит через центр описанной окружности треугольника АВС.

3. Докажите, что при любом n число 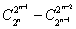делится на 4^n-1.

4. Имеется N человек, незнакомых между собой. Докажите, что при любом N их можно познакомить так, чтобы никакие трое не имели поровну знакомых.

5. Какое наибольшее число точек можно расположить на плоскости так, чтобы среди их попарных расстояний было бы только два различных?

6. Найдите все функции f(x), удовлетворяющие соотношению xf(y)+yf(x)=(x+y)f(x)f(y) при любых действительных x, y.

7. Пусть A,B,C - углы, a, b, c - стороны треугольника. Докажите неравенство .

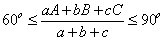8. Существует ли квадрат, вершины которого лежат на четырех концентрических окружностях, радиусы которых образуют арифметическую прогрессию?

Лига 11А

1. Вычислите сумму 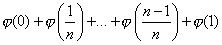, где .

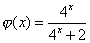2. Дан треугольник ABC. Две прямые, симметричные прямой АС относительно прямых АВ и ВС соответственно, пересекаются в точке К. Докажите, что прямая ВК проходит через центр описанной окружности треугольника АВС.

3. Докажите, что при любом n число 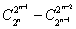делится на 4^n-1.

4. Имеется N человек, не знакомых между собой. Докажите, что при любом N их можно познакомить так, чтобы никакие трое не имели поровну знакомых.

5. Какое наибольшее число точек можно расположить на плоскости так, чтобы среди их попарных расстояний было бы только два различных?

6. Найдите все функции f(x), удовлетворяющие соотношению xf(y)+yf(x)=(x+y)f(x)f(y) при любых действительных x, y.

7. Пусть A,B,C - углы, a, b, c - стороны треугольника. Докажите неравенство .

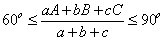8. Существует ли правильный шестиугольник , вершины которого лежат на шести концентрических сферах, радиусы которых образуют арифметическую прогрессию?

Полуфинальные бои

В полуфинале лиги 11А 19 ноября команда СУНЦ-11 встречалась с командой "57-11D" (капитан: Аня Боярченкова).

В упорной борьбе с итоговым счетом 50:36 победу одержала команда СУНЦ-11!

В другой полуфинальной паре команда Лицея "Вторая школа" одержала победу над командой Гимназии №1543.

Приведем условия задач:

1. Дан тетраэдр. 4 шара с центрами в его вершинах покрывают его весь. Вершины тетраэдра сдвинули так, что ни одно его ребро не увеличилось (радиусы шаров не изменились). Верно ли, что шары по-прежнему покрывают тетраэдр?

2. Двое играют на листе бумаги. Первый на своем ходе рисует кружок и, если хочет, соединяет его с некоторыми уже нарисованными кружками, но так, чтобы линии не пересекались (кружки, соединенные линиями, будем называть соседними); второй же ставит в этот кружок любое натуральное число, которое отличается от всех чисел в соседних кружках. Первый хочет заставить второго поставить число, большее девяти, а второй хочет обойтись только цифрами. Кто победит при правильной игре?

3. На некотором множестве действует операция x, удовлетворяющая условиям:
   – для любых A, B, C верно, что Ax(BxC)=Bx(CxA);
   – если AxB=AxC, то B=C.
   Докажите, что операция x коммутативна и ассоциативна.

4. Окружность радиуса 2006 не проходит через точки единичной решетки. Точка решетки называется граничной, если она и хотя бы одна из соседних с ней лежат по разные стороны окружности. Найдите разность между числом внешних и внутренних граничных точек.

5. Пусть M – середина стороны AD параллелограмма ABCD, N – проекция M на прямую BC, X – произвольная точка на продолжении отрезка CD за точку D, Y – точка пересечения прямых MX и AC. Докажите, что NM – биссектриса угла XNY.

6. Существует ли набор из 2006 различных натуральных чисел, в котором любые два числа взаимно просты, а сумма любых двух или более чисел – составное число?

7. Уравнение xⁿ+a₁x^n-1+...+a_k-1x^n-k+1+a_k+1x^n-k-1+...+a _n=0 имеет n действительных корней. Докажите, что a_k-1a_k+1<0.

8. Чемпион мира по волейболу определяется в однокруговом турнире n команд. Среди этих команд k, представляющих Европу, в играх между собой определяют чемпиона Европы. При каком наибольшем k команда, занявшая чистое первое место в чемпионате Европы, может занять чистое последнее место в чемпионате мира?

Финал

В финале лиги 11А 17 декабря команда СУНЦ-11 встречалась с командой "Л2Ш" (капитан: Лаут Илья).

Приведем условия задач:

1. В графе k ребер. Докажите, что в нем не более 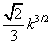треугольников.

2. Дана окружность и точка P внутри нее. Найдите геометрическое место вершин D равногранных тетраэдров ABCD, основание ABC которых вписано в данную окружность и имеет центр тяжести в точке P.

3. Дано n магнитофонных катушек, на которые намотаны ленты красными концами наружу, и 1 пустая катушка. При каких n можно перемотать все ленты так, чтобы каждая оказалась на своей катушке, но красным концом внутрь? (Перематывать можно с любой катушки на пустую в данный момент катушку, при этом наружный конец становится внутренним, и наоборот.)

4. Докажите для любых x, y, z Î [0,1] неравенство

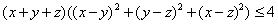
5. Докажите, что число 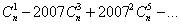(верхний индекс пробегает все нечетные значения, не превосходящие n) делится на 2^n-1.

6. "Инкубатор" - это прибор, позволяющий находить действительные корни любого кубического многочлена P(x). Как с его помощью найти корни многочлена P(P(x))-x?

7. Можно ли поместить куб в некоторый прямой круговой конус так, чтобы семь вершин куба лежали на боковой поверхности конуса?

8. Муха села в полдень на секундную стрелку часов и решила ездить, придерживаясь следующего правила: если одна стрелка обгоняет другую и муха сидит на одной из этих стрелок, то она пересаживается на другую. Сколько оборотов сделает муха к полуночи?

Решив на 2 задачи больше, заслуженную победу одержала команда Л2Ш. Таким образом,

команда СУНЦ - 11 заняла итоговое 2 место в турнире.